Minimax法
概要
- 別名:Minmax、saddle point
- 日)ミニマックス法、ミニマックス探索
- 最悪の場合で、想定される損失(Loss)が最小になるようにする決定ルール
- AI、ゲーム理論、統計学等で用いられる
- メリット
- 全ての場合の評価が可能
- 意思決定が容易
- デメリット
- 総当たり的に評価するため、処理に時間がかかる
AIでMinimaxアルゴリズムを利用する場合
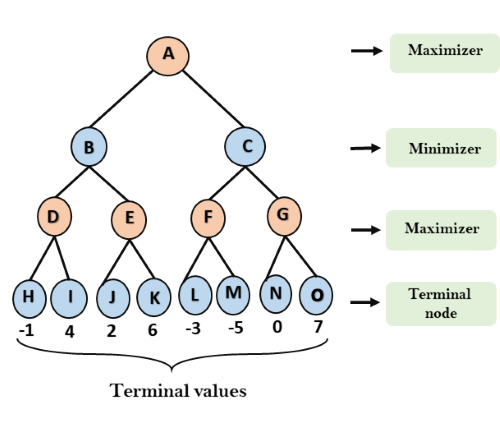
- 〇×ゲームやチェスなど、1対1かつ交互に意思決定を行って場の状態を変えていって最終的にどちらかのプレイヤーが勝利する場合、各ターンでどの意思決定をすればどちらが勝つのか、場の状態を全て考慮する
- ゲーム木を利用して意思決定方法を探索する
- 相手も最適なプレーをしていると仮定して、プレイヤーにとって最適な意思決定を提供する
Minimax定理
自身が取り得る戦略(ゲームの打ち手)の結果として損失(マイナスの利得)が最大(マキシマム)なもの同士を比較して、その中から最小(ミニマム)の戦略を選択する行動原理
https://www.itmedia.co.jp/im/articles/0901/08/news149.html
- 1926年にJohn von Neumannによって示された、ゲーム理論の最も標準形となる“ゼロサム2人ゲーム”の主要定理
Pseudocode
function minimax(node, depth, maximizingPlayer) is
if depth = 0 or node is a terminal node then
return the heuristic value of node
if maximizingPlayer then
value := −∞
for each child of node do
value := max(value, minimax(child, depth − 1, FALSE))
return value
else (* minimizing player *)
value := +∞
for each child of node do
value := min(value, minimax(child, depth − 1, TRUE))
return value